We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Previous results by the author on the connection between three measures of noncompactness obtained for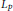 
${{\mathcal{L}}_{p}}$ are extended to regular spaces of measurable functions. An example is given of the advantages of some cases in comparison with others. Geometric characteristics of regular spaces are determined. New theorems for 
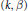$\left( k,\,\beta \right)$-boundedness of partially additive operators are proved.
