We systematically study conservation theorems on theories of semi-classical arithmetic, which lie in-between classical arithmetic $\mathsf {PA}$ and intuitionistic arithmetic $\mathsf {HA}$. Using a generalized negative translation, we first provide a structured proof of the fact that $\mathsf {PA}$ is $\Pi _{k+2}$-conservative over $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$ where ${\Sigma _k}\text {-}\mathrm {LEM}$ is the axiom scheme of the law-of-excluded-middle restricted to formulas in $\Sigma _k$. In addition, we show that this conservation theorem is optimal in the sense that for any semi-classical arithmetic T, if $\mathsf {PA}$ is $\Pi _{k+2}$-conservative over T, then ${T}$ proves ${\Sigma _k}\text {-}\mathrm {LEM}$. In the same manner, we also characterize conservation theorems for other well-studied classes of formulas by fragments of classical axioms or rules. This reveals the entire structure of conservation theorems with respect to the arithmetical hierarchy of classical principles.

We extend the usual language of second order arithmetic to one in which we can discuss an ultrafilter over of the sets of a given model. The semantics are based on fixing a subclass of the sets in a structure for the basic language that corresponds to the intended ultrafilter. In this language we state axioms that express the notion that the subclass is an ultrafilter and additional ones that say it is idempotent or Ramsey. The axioms for idempotent ultrafilters prove, for example, Hindman’s theorem and its generalizations such as the Galvin--Glazer theorem and iterated versions of these theorems (IHT and IGG). We prove that adding these axioms to IHT produce conservative extensions of ACA0 +IHT, 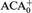${\rm{ACA}}_{\rm{0}}^ +$, ATR0, 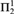${\rm{\Pi }}_2^1$-CA0, and 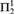${\rm{\Pi }}_2^1$-CA0 for all sentences of second order arithmetic and for full Z2 for the class of 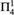${\rm{\Pi }}_4^1$ sentences. We also generalize and strengthen a metamathematical result of Wang (1984) to show, for example, that any 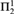${\rm{\Pi }}_2^1$ theorem ∀X∃YΘ(X,Y) provable in ACA0 or 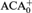${\rm{ACA}}_{\rm{0}}^ +$ there are e,k ∈ ℕ such that ACA0 or 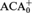${\rm{ACA}}_{\rm{0}}^ +$ proves that ∀X(Θ(X, Φe(J(k)(X))) where Φe is the eth Turing reduction and J(k) is the kth iterate of the Turing or Arithmetic jump, respectively. (A similar result is derived for 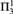${\rm{\Pi }}_3^1$ theorems of 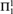${\rm{\Pi }}_1^1$-CA0 and the hyperjump.)