In this note we prove that the local martingale part of a convex functionf of a d-dimensional semimartingaleX = M + A can be written in terms ofan Itô stochastic integral∫H(X)dM, whereH(x) is some particular measurable choice ofsubgradient \hbox{$\sub$}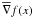$\overline{\mathrm{\nabla }}\mathit{f}\mathrm{\left(}\mathit{x}\mathrm{\right)}$ off at x, and M is the martingale partof X. This result was first proved by Bouleau in [N. Bouleau, C.R. Acad. Sci. Paris Sér. I Math. 292 (1981) 87–90]. Here wepresent a new treatment of the problem. We first prove the result for\hbox{$\widetilde{X}=X+\epsilon B$}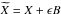$\begin{array}{}{}_{\mathrm{􏽥}}\\ \mathit{X}\end{array}\mathrm{=}\mathit{X}\mathrm{+}\mathit{ϵB}$,ϵ > 0, where B is a standardBrownian motion, and then pass to the limit as ϵ → 0, using results in[M.T. Barlow and P. Protter, On convergence of semimartingales. In Séminaire deProbabilités, XXIV, 1988/89, Lect. Notes Math., vol. 1426.Springer, Berlin (1990) 188–193; E. Carlen and P. Protter, Illinois J. Math.36 (1992) 420–427]. The former paper concerns convergence ofsemimartingale decompositions of semimartingales, while the latter studies a special caseof converging convex functions of semimartingales.

We present a general closed 4-point quadrature rule based on Euler-type identities. We use this rule to prove a generalization of Hadamard's inequalities for (2r)-convex functions (r ≥ 1).