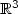1 results
On the curvature and torsion effects inone dimensional waveguides
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 05 September 2007, pp. 793-808
- Print publication:
- October 2007
-
- Article
- Export citation
-
We consider the Laplace operator in a thin tube of ${\mathbb R}^3$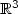
with a Dirichlet condition on its boundary. We study asymptotically the spectrum ofsuch an operator as the thickness of the tube's cross section goes to zero. In particular weanalyse how the energy levels depend simultaneously on the curvature of the tube's central axisand on the rotation of the cross section with respect to the Frenet frame. The main argument is aΓ-convergence theorem for a suitable sequence of quadratic energies.
