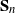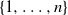We study an example of a hit-and-run random walk on the symmetric group $\mathbf S_n$ . Our starting point is the well-understood top-to-random shuffle. In the hit-and-run version, at each single step, after picking the point of insertion j uniformly at random in $\{1,\ldots,n\}$ , the top card is inserted in the jth position k times in a row, where k is uniform in 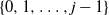$\{0,1,\ldots,j-1\}$ . The question is, does this accelerate mixing significantly or not? We show that, in 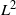$L^2$ and sup-norm, this accelerates mixing at most by a constant factor (independent of n). Analyzing this problem in total variation is an interesting open question. We show that, in general, hit-and-run random walks on finite groups have non-negative spectrum.

We consider the sequence of powers of a positive definite function on a discrete group. Taking inspiration from random walks on compact quantum groups, we give several examples of situations where a cut-off phenomenon occurs for this sequence, including free groups and infinite Coxeter groups. We also give examples of absence of cut-off using free groups again.

Consider a population of fixed size consisting of N haploid individuals. Assume that this population evolves according to the two-allele neutral Moran model in mathematical genetics. Denote the two alleles by A1 and A2. Allow mutation from one type to another and let 0 < γ < 1 be the sum of mutation probabilities. All the information about the population is recorded by the Markov chain X = (X(t))t≥0 which counts the number of individuals of type A1. In this paper we study the time taken for the population to ‘reach’ stationarity (in the sense of separation and total variation distances) when initially all individuals are of one type. We show that after t∗ = Nγ-1logN + cN the separation distance between the law of X(t∗) and its stationary distribution converges to 1 - exp(-γe-γc) as N → ∞. For the total variation distance an asymptotic upper bound is obtained. The results depend on a particular duality, and couplings, between X and a genealogical process known as the lines of descent process.