An explicit formula forthe mean value of 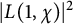$\vert L(1,\chi )\vert ^2$ is known, where 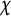$\chi $ runs over all odd primitive Dirichlet characters of prime conductors p. Bounds on the relative class number of the cyclotomic field 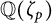${\mathbb Q}(\zeta _p)$ follow. Lately, the authors obtained that the mean value of 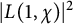$\vert L(1,\chi )\vert ^2$ is asymptotic to 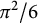$\pi ^2/6$, where 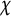$\chi $ runs over all odd primitive Dirichlet characters of prime conductors 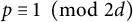$p\equiv 1\ \ \pmod {2d}$ which are trivial on a subgroup H of odd order d of the multiplicative group 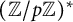$({\mathbb Z}/p{\mathbb Z})^*$, provided that 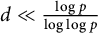$d\ll \frac {\log p}{\log \log p}$. Bounds on the relative class number of the subfield of degree 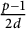$\frac {p-1}{2d}$ of the cyclotomic field 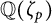${\mathbb Q}(\zeta _p)$ follow. Here, for a given integer 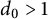$d_0>1$, we consider the same questions for the nonprimitive odd Dirichlet characters 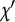$\chi '$ modulo 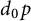$d_0p$ induced by the odd primitive characters 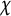$\chi $ modulo p. We obtain new estimates for Dedekind sums and deduce that the mean value of 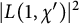$\vert L(1,\chi ')\vert ^2$ is asymptotic to 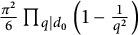$\frac {\pi ^2}{6}\prod _{q\mid d_0}\left (1-\frac {1}{q^2}\right )$, where 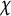$\chi $ runs over all odd primitive Dirichlet characters of prime conductors p which are trivial on a subgroup H of odd order 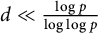$d\ll \frac {\log p}{\log \log p}$. As a consequence, we improve the previous bounds on the relative class number of the subfield of degree 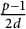$\frac {p-1}{2d}$ of the cyclotomic field 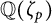${\mathbb Q}(\zeta _p)$. Moreover, we give a method to obtain explicit formulas and use Mersenne primes to show that our restriction on d is essentially sharp.

The Euler–Mascheroni constant $\gamma =0.5772\ldots \!$ is the $K={\mathbb Q}$ example of an Euler–Kronecker constant $\gamma _K$ of a number field $K.$ In this note, we consider the size of the $\gamma _q=\gamma _{K_q}$ for cyclotomic fields $K_q:={\mathbb Q}(\zeta _q).$ Assuming the Elliott–Halberstam Conjecture (EH), we prove uniformly in Q that

$$ \begin{align*} \frac{1}{Q}\sum_{Q<q\le 2Q} |{\gamma_q - \log q}| = o(\log Q).\end{align*} $$

In other words, under EH, the $\gamma _q /\!\log q$ in these ranges converge to the one point distribution at $1$ . This theorem refines and extends a previous result of Ford, Luca and Moree for prime $q.$ The proof of this result is a straightforward modification of earlier work of Fouvry under the assumption of EH.

A Ducci sequence is a sequence of integer $n$-tuples generated by iterating the map

$$\begin{eqnarray}D:(a_{1},a_{2},\ldots ,a_{n})\mapsto (|a_{1}-a_{2}|,|a_{2}-a_{3}|,\ldots ,|a_{n}-a_{1}|).\end{eqnarray}$$

$P(n)$

$n$

$n$

$p\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$

$2$

$x^{2}-py^{2}=-4$

$x$

$y$

In this paper, we give a general explicit form of Cassels’ $p$-adic embedding theorem for number fields. We also give its refined form in the case of cyclotomic fields. As a byproduct, given an irreducible polynomial $f$ over $\mathbb{Z}$, we give a general unconditional upper bound for the smallest prime number $p$ such that $f$ has a simple root modulo $p$.

Let D be a division algebra whose class [D] is in B(K), the Brauer group of an algebraic number field K. If [D⊗KL] is the trivial class in B(L), then we say that L is a splitting field for D or L splits D. The splitting fields in D of smallest dimension are the maximal subfields of D. Although there are infinitely many maximal subfields of D which are cyclic extensions of K; from the perspective of the Schur Subgroup S(K) of B(K) the natural splitting fields are the cyclotomic ones. In (Cyclotomic Splitting Fields, Proc. Amer. Math. Soc. 25 (1970), 630-633) there are errors which have led to the main result of this paper, namely to provide necessary and sufficient conditions for (D) in S(K) to have a maximal subfield which is a cyclic cyclotomic extension of K, a finite abelian extension of Q. A similar result is provided for quaternion division algebras in B(K).