1 results
Functorial destackification of tame stacks with abelian stabilisers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1257-1315
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
-
We give an algorithm for removing stackiness from smooth, tame Artin stacks with abelian stabilisers by repeatedly applying stacky blow-ups. The construction works over a general base and is functorial with respect to base change and compositions with gerbes and smooth, stabiliser-preserving maps. As applications, we indicate how the result can be used for destackifying general Deligne–Mumford stacks in characteristic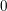
$0$, and to obtain a weak factorisation theorem for such stacks. Over an arbitrary field, the method can be used to obtain a functorial algorithm for desingularising varieties with simplicial toric quotient singularities, without assuming the presence of a toroidal structure.
