1 results
On the equidistribution of unstable curves for pseudo-Anosov diffeomorphisms of compact surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 855-880
- Print publication:
- March 2022
-
- Article
- Export citation
-
We prove that the asymptotics of ergodic integrals along an invariant foliation of a toral Anosov diffeomorphism, or of a pseudo-Anosov diffeomorphism on a compact orientable surface of higher genus, is determined (up to a logarithmic error) by the action of the diffeomorphism on the cohomology of the surface. As a consequence of our argument and of the results of Giulietti and Liverani [Parabolic dynamics and anisotropic Banach spaces. J. Eur. Math. Soc. (JEMS)21(9) (2019), 2793–2858] on horospherical averages, toral Anosov diffeomorphisms have no Ruelle resonances in the open interval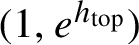
$(1, e^{h_{\mathrm {top}}})$
.
