For $R(z, w)\in \mathbb {C}(z, w)$ of degree at least 2 in w, we show that the number of rational functions $f(z)\in \mathbb {C}(z)$ solving the difference equation $f(z+1)=R(z, f(z))$ is finite and bounded just in terms of the degrees of R in the two variables. This complements a result of Yanagihara, who showed that any finite-order meromorphic solution to this sort of difference equation must be a rational function. We prove a similar result for the differential equation $f'(z)=R(z, f(z))$ , building on a result of Eremenko.

Let P and Q be relatively prime integers greater than 1, and let f be a real valued discretely supported function on a finite dimensional real vector space V. We prove that if $f_{P}(x)=f(Px)-f(x)$ and $f_{Q}(x)=f(Qx)-f(x)$ are both $\Lambda $ -periodic for some lattice $\Lambda \subset V$ , then so is f (up to a modification at $0$ ). This result is used to prove a theorem on the arithmetic of elliptic function fields. In the last section, we discuss the higher rank analogue of this theorem and explain why it fails in rank 2. A full discussion of the higher rank case will appear in a forthcoming work.

In this paper, we study the stability in the Lyapunov sense of the equilibrium solutions of discrete or difference Hamiltonian systems in the plane. First, we perform a detailed study of linear Hamiltonian systems as a function of the parameters. In particular we analyze the regular and the degenerate cases. Next, we give a detailed study of the normal form associated with the linear Hamiltonian system. At the same time we obtain the conditions under which we can get stability (in linear approximation) of the equilibrium solution, classifying all the possible phase diagrams as a function of the parameters. After that, we study the stability of the equilibrium solutions of the first order difference system in the plane associated with mechanical Hamiltonian systems and Hamiltonian systems defined by cubic polynomials. Finally, we point out important differences with the continuous case.

This paper addresses the problem of trajectory tracking control in mobile robots under velocity limitations. Following the results reported in ref. [1], the problem of trajectory tracking considering control actions constraint is focused and the zero convergence of the tracking errors is demonstrated. In this work, the original methodology is expanded considering a controller that depends not only on the position but also on the velocity. A simple scheme is obtained, which can be easily implemented in others controllers of the literature. Experimental results are presented and discussed, demonstrating the good performance of the controller.

We study an atomistic pair potential-energy E (n)(y) that describesthe elastic behavior of two-dimensional crystals with n atoms where $y \in {\mathbb R}^{2\times n}$ 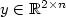characterizes the particle positions. The mainfocus is the asymptotic analysis of the ground state energy as ntends to infinity. We show in a suitable scaling regime where theenergy is essentially quadratic that the energy minimum of E (n)admits an asymptotic expansion involving fractional powers of n:

${\rm min}_y E^{(n)}(y) = n \, E_{\mathrm{bulk}}+ \sqrt{n} \, E_\mathrm{surface} +o(\sqrt{n}), \qquad n \to \infty.$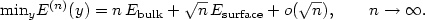

The bulk energy density E bulk is given by an explicitexpression involving the interaction potentials. The surface energyE surface can be expressed as a surface integral where theintegrand depends only on the surface normal and the interactionpotentials. The evaluation of the integrand involves solving a discrete algebraic Riccati equation. Numerical simulations suggestthat the integrand is a continuous, but nowhere differentiable function ofthe surface normal.

We obtain inverse factorial-series solutions of second-order linear difference equations with a singularity of rank one at infinity. It is shown that the Borel plane of these series is relatively simple, and that in certain cases the asymptotic expansions incorporate simple resurgence properties. Two examples are included. The second example is the large $a$ asymptotics of the hypergeometric function ${}_2F_1(a,b;c;x)$.

AMS 2000 Mathematics subject classification: Primary 34E05; 39A11. Secondary 33C05

In time series analysis, it is well-known that the differencing operator ∇d may transform a non-stationary series, {Z(t)} say, to a stationary one, {W(t)} = ∇dZ(t)}; and there are many procedures for analysing and modelling {Z(t)} which exploit this transformation. Rather differently, Matheron (1973) introduced a set of measures on Rn that transform an appropriate non-stationary spatial process to stationarity, and Cressie (1988) then suggested that specialized low-order analogues of these measures, called increment-vectors, be used in time series analysis. This paper develops a general theory of increment-vectors which provides a more powerful transformation tool than mere simple differencing. The methodology gives a handle on the second-moment structure and divergence behaviour of homogeneously non-stationary series which leads to many important applications such as determining the correct degree of differencing, forecasting and interpolation.

We study the stability of linear filters associated with certain types of linear difference equations with variable coefficients. We show that stability is determined by the locations of the poles of a rational transfer function relative to the spectrum of an associated weighted shift operator. The known theory for filters associated with constant-coefficient difference equations is a special case.

Learning from Matheron's representation (1973), and using the increment vector (PIV) methodology introduced by Cressie (1988) and developed by Chen and Anderson (1994), this paper presents a theory for the representation and decomposition of integrated stationary time series and gives some applications.