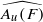The Poisson and Martin boundaries for invariant random walks on the dual of the orthogonal quantum groups $A_{\mathrm{o}}(F)$ are identified with higher-dimensional Podleś spheres that we describe in terms of generators and relations. This provides the first such identification for random walks on non-amenable discrete quantum groups.