1 results
Lipschitz-free spaces and subsets of finite-dimensional spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We consider two questions on the geometry of Lipschitz-free $p$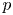
-spaces $\mathcal {F}_p$
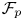, where $0< p\leq 1$
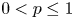, over subsets of finite-dimensional vector spaces. We solve an open problem and show that if $(\mathcal {M}, \rho )$
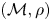is an infinite doubling metric space (e.g. an infinite subset of an Euclidean space), then $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )\simeq \ell _p$
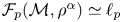for every $\alpha \in (0,\,1)$
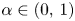and $0< p\leq 1$
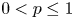. An upper bound on the Banach–Mazur distance between the spaces $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$
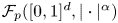and $\ell _p$
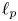is given. Moreover, we tackle a question due to Albiac et al. [4] and expound the role of $p$
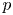, $d$
for the Lipschitz constant of a canonical, locally coordinatewise affine retraction from $(K, |\cdot |_1)$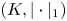
, where $K=\cup _{Q\in \mathcal {R}} Q$
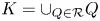is a union of a collection $\emptyset \neq \mathcal {R} \subseteq \{ Rw + R[0,\,1]^d: w\in \mathbb {Z}^d\}$
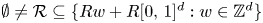of cubes in $\mathbb {R}^d$
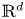with side length $R>0$
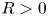, into the Lipschitz-free $p$
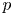-space $\mathcal {F}_p (V, |\cdot |_1)$
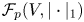over their vertices.
