The Probably Approximately Correct (PAC) learning is a machine learning model introduced by Leslie Valiant in 1984. The PACi reducibility refers to the PAC reducibility independent of size and computation time. This reducibility in PAC learning resembles the reducibility in Turing computability. The ordering of concept classes under PAC reducibility is nonlinear, even when restricted to particular concrete examples.
Due to the resemblance to Turing Reducibility, we suspected that there could be incomparable PACi and PAC degrees for the PACi and PAC reducibilities as in Turing incomparable degrees. In 1957 Friedberg and in 1956 Muchnik independently solved the Post problem by constructing computably enumerable sets A and B of incomparable degrees using the priority construction method. We adapt this idea to PACi and PAC reducibilities and construct two effective concept classes C and D such that C is not reducible to D and vice versa. When considering PAC reducibility it was necessary to work on the size of an effective concept class, thus we use Kolmogorov complexity to obtain the size. The non-learnability of concept classes in the PAC learning model is explained by the existence of PAC incomparable degrees.
Analogous to the Turing jump, we give a jump operation on effective concept classes for the zero jump. To define the zero jump operator for PACi degrees the join of all the effective concept classes is constructed and proved that it is a greatest element. There are many properties proven for existing degrees. Thus we can explore proving those properties to PACi and PAC degrees. But if we prove an embedding from those degrees to PACi and PAC degrees then those properties will be true for PACi and PAC degrees without explicitly proving them.
Abstract prepared by Dodamgodage Gihnee M. Senadheera and taken directly from the thesis
E-mail: senadheerad@winthrop.edu
URL: https://www.proquest.com/docview/2717762461/abstract/ACD19F29A8774AF6PQ/1?accountid=13864
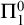 $\Pi ^0_1$ CLASSES
$\Pi ^0_1$ CLASSES