At high temperature, MgAl2O4 spinel is stabilized by disorder of Mg and Al between octahedral and tetrahedral sites. This behaviour has been measured up to 1700 K in recent neutron experiments, but the extrapolation of subsequently fitted thermodynamic models is not reliable. First principles simulation of the electronic structure of such minerals can in principle accurately predict disorder, but would require unfeasibly large computing resources. We have instead parameterized on-site and short-ranged cluster potentials using a small number of electronic structure simulations at zero temperature. These potentials were then used in large-scale statistical simulations at finite temperatures to predict disordering thermodynamics beyond the range of experimental measurements. Within the temperature range of the experiment, good agreement is obtained for the degree of order. The entropy and free energy are calculated and compared to those from macroscopic models.

In this article, we provide a priori error estimates for the spectral andpseudospectral Fourier (also called planewave) discretizations of theperiodic Thomas-Fermi-von Weizsäcker (TFW) model and for the spectraldiscretization of the periodic Kohn-Shammodel, within the local density approximation (LDA). These modelsallow to compute approximations of the electronic ground state energy and densityof molecular systems in the condensed phase. The TFW model is strictlyconvex with respect to the electronic density, and allows for acomprehensive analysis. This is not the case for the Kohn-Sham LDAmodel, for which the uniqueness of the ground state electronic densityis not guaranteed. We prove that, for any local minimizer $\Phi^0$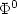 of the Kohn-Sham LDA model, and under a coercivity assumption ensuring the local uniqueness of this minimizer up to unitary transform, the discretized Kohn-Sham LDA problem has a minimizer in the vicinity of $\Phi^0$ 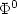for large enough energy cut-offs, and that this minimizer is unique up to unitary transform. We then derive optimal a priori error estimates for the spectral discretization method.

The Conjugate Orthogonal Conjugate Residual (COCR) method [T. Sogabe and S.-L. Zhang, JCAM, 199 (2007), pp. 297-303.] has recently been proposed for solving complex symmetric linear systems. In the present paper, we develop a variant of the COCR method that allows the efficient solution of complex symmetric shifted linear systems. Some numerical examples arising from large-scale electronic structure calculations are presented to illustrate the performance of the variant.