We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate the distribution of the digits of quotients of randomly chosen positive integers taken from the interval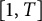 
$[1,T]$
, improving the previously known error term for the counting function as 
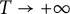$T\to +\infty $
. We also resolve some natural variants of the problem concerning points with prime coordinates and points that are visible from the origin.
