We propose and analyse an alternate approach to a priori error estimates for the semidiscrete Galerkin approximation to a time-dependent parabolic integro-differential equation with nonsmooth initial data. The method is based on energy arguments combined with repeated use of time integration, but without using parabolic-type duality techniques. An optimal  $L^2$-error estimate is derived for the semidiscrete approximation when the initial data is in
$L^2$-error estimate is derived for the semidiscrete approximation when the initial data is in 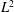 $L^2$. A superconvergence result is obtained and then used to prove a maximum norm estimate for parabolic integro-differential equations defined on a two-dimensional bounded domain.
$L^2$. A superconvergence result is obtained and then used to prove a maximum norm estimate for parabolic integro-differential equations defined on a two-dimensional bounded domain.
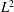 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA