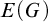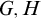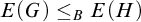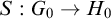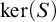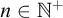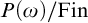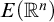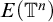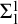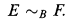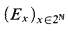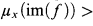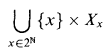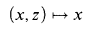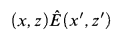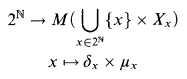7 results
Borel reducibility of equivalence relations on
 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 687-700
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY LOCALLY COMPACT ABELIAN POLISH GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
DEGREE SPECTRA OF ANALYTIC COMPLETE EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1663-1676
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EQUIVALENCE RELATIONS GENERATED BY SCHAUDER BASES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1459-1481
- Print publication:
- December 2017
-
- Article
- Export citation
EMBEDDINGS OF P(ω)/Fin INTO BOREL EQUIVALENCE RELATIONS BETWEEN ℓp AND ℓq
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 July 2015, pp. 917-939
- Print publication:
- September 2015
-
- Article
- Export citation
On enveloping type-definable structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 76 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1023-1034
- Print publication:
- September 2011
-
- Article
- Export citation
Bi-Borel reducibility of essentially countable Borel equivalence relations
-
- Journal:
- The Journal of Symbolic Logic / Volume 70 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 12 March 2014, pp. 979-992
- Print publication:
- September 2005
-
- Article
- Export citation