We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we study the notion of equivariant forms introduced in the authors' previous works. In particular, we completely classify all the equivariant forms for a subgroup of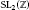 
$\text{S}{{\text{L}}_{2\left( \mathbb{Z} \right)}}$ by means of the cross-ratio, weight 2 modular forms, quasimodular forms, as well as differential forms of a Riemann surface and sections of a canonical line bundle.
