We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Posterior odds of cheating on achievement tests are presented as an alternative to \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$p$$\end{document}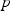
values reported for statistical hypothesis testing for several of the probabilistic models in the literature on the detection of cheating. It is shown how to calculate their combinatorial expressions with the help of a reformulation of the simple recursive algorithm for the calculation of number-correct score distributions used throughout the testing industry. Using the odds avoids the arbitrary choice between statistical tests of answer copying that do and do not condition on the responses the test taker is suspected to have copied and allows the testing agency to account for existing circumstantial evidence of cheating through the specification of prior odds.
