We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We determine the asymptotic behavior of the higher dimensional Reidemeister torsion for the graph manifolds obtained by exceptional surgeries along twist knots. We show that all irreducible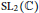 
$\text{S}{{\text{L}}_{2}}(\mathbb{C})$-representations of the graph manifold are induced by irreducible metabelian representations of the twist knot group. We also give the set of the limits of the leading coeõcients in the higher dimensional Reidemeister torsion explicitly.
