1 results
ON THE EXPECTED UNIFORM ERROR OF BROWNIAN MOTION APPROXIMATED BY THE LÉVY–CIESIELSKI CONSTRUCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 581-593
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
The Brownian bridge or Lévy–Ciesielski construction of Brownian paths almost surely converges uniformly to the true Brownian path. We focus on the uniform error. In particular, we show constructively that at level N, at which there are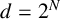
$d=2^N$ points evaluated on the Brownian path, the uniform error and its square, and the uniform error of geometric Brownian motion, have upper bounds of order 
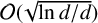$\mathcal {O}(\sqrt {\ln d/d})$, matching the known orders. We apply the results to an option pricing example.
