The paper is devoted to the convergence analysis of a well-knowncell-centered Finite Volume Method (FVM) for aconvection-diffusion problem in $\mathbb{R}^2$ 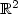 . This FVM is based on Voronoi boxes andexponential fitting. To prove the convergence of the FVM, we usea new nonconforming Petrov-Galerkin Finite Element Method (FEM)for which the system of linear equations coincides completely withthat of the FVM. Thus, by proving convergence properties of theFEM we obtain similar ones for the FVM. For the error estimationof the FEM well-known statements have to be modified.
. This FVM is based on Voronoi boxes andexponential fitting. To prove the convergence of the FVM, we usea new nonconforming Petrov-Galerkin Finite Element Method (FEM)for which the system of linear equations coincides completely withthat of the FVM. Thus, by proving convergence properties of theFEM we obtain similar ones for the FVM. For the error estimationof the FEM well-known statements have to be modified.