An a priori Campanato type regularity condition is established for a class of W1X local minimisers $\overline{u}$ 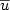 of the general variational integral $\int_{\Omega} F(\nabla u(x))\,{\rm d}x$
of the general variational integral $\int_{\Omega} F(\nabla u(x))\,{\rm d}x$ 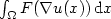 where $\Omega \subset \mathbb{R}^n$
where $\Omega \subset \mathbb{R}^n$ 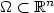 is an open bounded domain, F is of class C2, F is strongly quasi-convex and satisfies the growth condition $F(\xi)\leq c(1+|\xi|^p)$
is an open bounded domain, F is of class C2, F is strongly quasi-convex and satisfies the growth condition $F(\xi)\leq c(1+|\xi|^p)$ 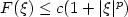 for a p > 1 and where the corresponding Banach spaces X are the Morrey-Campanato space $\mathcal{L}^{p,\mu} (\Omega,\mathbb{R}^{N\times n})$
for a p > 1 and where the corresponding Banach spaces X are the Morrey-Campanato space $\mathcal{L}^{p,\mu} (\Omega,\mathbb{R}^{N\times n})$ 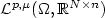 , µ < n, Campanato space $\mathcal{L}^{p,n}(\Omega,\mathbb{R}^{N\times n})$
, µ < n, Campanato space $\mathcal{L}^{p,n}(\Omega,\mathbb{R}^{N\times n})$ 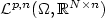 and the space of bounded mean oscillation $ {\rm BMO}\Omega,\mathbb{R}^{N\times n})$
and the space of bounded mean oscillation $ {\rm BMO}\Omega,\mathbb{R}^{N\times n})$ 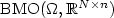 . The admissible maps $u\colon \Omega \to \mathbb{R}^N$
. The admissible maps $u\colon \Omega \to \mathbb{R}^N$ 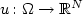 are of Sobolev class W1,p , satisfying a Dirichlet boundary condition, and to help clarify the significance of the above result the sufficiency condition for W1BMO local minimisers is extended from Lipschitz maps to this admissible class.
are of Sobolev class W1,p , satisfying a Dirichlet boundary condition, and to help clarify the significance of the above result the sufficiency condition for W1BMO local minimisers is extended from Lipschitz maps to this admissible class.