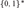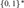1 results
BROUWER’S FAN THEOREM AND CONVEXITY
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1363-1375
- Print publication:
- December 2018
-
- Article
- Export citation
-
In the framework of Bishop’s constructive mathematics we introduce co-convexity as a property of subsets B of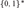
${\left\{ {0,1} \right\}^{\rm{*}}}$, the set of finite binary sequences, and prove that co-convex bars are uniform. Moreover, we establish a canonical correspondence between detachable subsets B of 
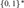${\left\{ {0,1} \right\}^{\rm{*}}}$ and uniformly continuous functions f defined on the unit interval such that B is a bar if and only if the corresponding function f is positive-valued, B is a uniform bar if and only if f has positive infimum, and B is co-convex if and only if f satisfies a weak convexity condition.
