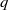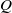The paperfolding sequences form an uncountable class of infinite sequences over the alphabet  $\{ -1, 1 \}$ that describe the sequence of folds arising from iterated folding of a piece of paper, followed by unfolding. In this note, we observe that the sequence of run lengths in such a sequence, as well as the starting and ending positions of the nth run, is
$\{ -1, 1 \}$ that describe the sequence of folds arising from iterated folding of a piece of paper, followed by unfolding. In this note, we observe that the sequence of run lengths in such a sequence, as well as the starting and ending positions of the nth run, is  $2$-synchronised and hence computable by a finite automaton. As a specific consequence, we obtain the recent results of Bunder, Bates and Arnold [‘The summed paperfolding sequence’, Bull. Aust. Math. Soc. 110 (2024), 189–198] in much more generality, via a different approach. We also prove results about the critical exponent and subword complexity of these run-length sequences.
$2$-synchronised and hence computable by a finite automaton. As a specific consequence, we obtain the recent results of Bunder, Bates and Arnold [‘The summed paperfolding sequence’, Bull. Aust. Math. Soc. 110 (2024), 189–198] in much more generality, via a different approach. We also prove results about the critical exponent and subword complexity of these run-length sequences.