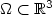We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The incompressible MHD equations couple Navier-Stokes equations with Maxwell's equationsto describe the flow of a viscous, incompressible, and electrically conducting fluid ina Lipschitz domain $\Omega \subset \mathbb{R}^3$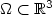 
.We verify convergence of iterates of different coupling anddecoupling fully discrete schemes towards weak solutions forvanishing discretization parameters. Optimal first order of convergence is shown in the presence of strong solutions for a splitting scheme which decouplesthe computation of velocity field, pressure, and magnetic fields atevery iteration step.
