A result of Haglund implies that the 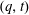$(q,t)$-bigraded Hilbert series of the space of diagonal harmonics is a 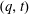$(q,t)$-Ehrhart function of the flow polytope of a complete graph with netflow vector 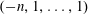$(-n,1,\ldots ,1)$. We study the 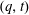$(q,t)$-Ehrhart functions of flow polytopes of threshold graphs with arbitrary netflow vectors. Our results generalize previously known specializations of the mentioned bigraded Hilbert series at 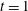$t=1$, 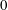$0$, and 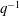$q^{-1}$. As a corollary to our results, we obtain a proof of a conjecture of Armstrong, Garsia, Haglund, Rhoades, and Sagan about the 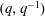$(q,q^{-1})$-Ehrhart function of the flow polytope of a complete graph with an arbitrary netflow vector.

Toric quiver varieties (moduli spaces of quiver representations) are studied. Given a quiver and a weight, there is an associated quasi-projective toric variety together with a canonical embedding into projective space. It is shown that for a quiver with no oriented cycles the homogeneous ideal of this embedded projective variety is generated by elements of degree at most 3. In each fixed dimension d up to isomorphism there are only finitely many d-dimensional toric quiver varieties. A procedure for their classification is outlined.