We show that there are no non-trivial stratified bundles over a smooth simply connected quasi-projective variety over an algebraic closure of a finite field if the variety admits a normal projective compactification with boundary locus of codimension greater than or equal to 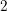 $2$.
$2$.
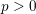 $p>0$
$p>0$