1 results
Deformations of corank 1 frontals
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1204-1234
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We develop a Thom–Mather theory of frontals analogous to Ishikawa's theory of deformations of Legendrian singularities but at the frontal level, avoiding the use of the contact setting. In particular, we define concepts like frontal stability, versality of frontal unfoldings or frontal codimension. We prove several characterizations of stability, including a frontal Mather–Gaffney criterion, and of versality. We then define the method of reduction with which we show how to construct frontal versal unfoldings of plane curves and show how to construct stable unfoldings of corank 1 frontals with isolated instability which are not necessarily versal. We prove a frontal version of Mond's conjecture in dimension 1. Finally, we classify stable frontal multigerms and give a complete classification of corank 1 stable frontals from $\mathbb {C}^3$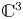
to $\mathbb {C}^4$
.
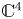