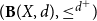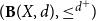In this paper, we study quasi-metric spaces using domain theory. Given a quasi-metric space (X,d), we use $({\bf B}(X,d),\leq^{d^{+}}\!)$ to denote the poset of formal balls of the associated quasi-metric space (X,d). We introduce the notion of local Yoneda-complete quasi-metric spaces in terms of domain-theoretic properties of $({\bf B}(X,d),\leq^{d^{+}}\!)$ . The manner in which this definition is obtained is inspired by Romaguera–Valero theorem and Kostanek–Waszkiewicz theorem. Furthermore, we obtain characterizations of local Yoneda-complete quasi-metric spaces via local nets in quasi-metric spaces. More precisely, we prove that a quasi-metric space is local Yoneda-complete if and only if every local net has a d-limit. Finally, we prove that every quasi-metric space has a local Yoneda completion.