We compute the gap distribution of directions of saddle connections for two classes of translation surfaces. One class will be the translation surfaces arising from gluing two identical tori along a slit. These yield the first explicit computations of gap distributions for non-lattice translation surfaces. We show that this distribution has support at zero and quadratic tail decay. We also construct examples of translation surfaces in any genus 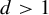$d>1$ that have the same gap distribution as the gap distribution of two identical tori glued along a slit. The second class we consider are twice-marked tori and saddle connections between distinct marked points with a specific orientation. These results can be interpreted as the gap distribution of slopes of affine lattices. We obtain our results by translating the question of gap distributions to a dynamical question of return times to a transversal under the horocycle flow on an appropriate moduli space.