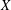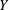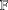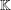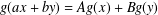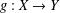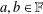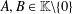1 results
A NOTE ON THE GENERALISED HYPERSTABILITY OF THE GENERAL LINEAR EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 263-273
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
-
Let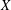
$X$ and 
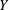$Y$ be two normed spaces over fields 
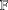$\mathbb{F}$ and 
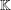$\mathbb{K}$, respectively. We prove new generalised hyperstability results for the general linear equation of the form 
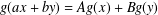$g(ax+by)=Ag(x)+Bg(y)$, where 
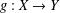$g:X\rightarrow Y$ is a mapping and 
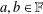$a,b\in \mathbb{F}$, 
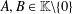$A,B\in \mathbb{K}\backslash \{0\}$, using a modification of the method of Brzdęk [‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl.2013 (2013), Art. ID 285, 9 pages]. The hyperstability results of Piszczek [‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc.52 (2015), 1827–1838] can be derived from our main result.
