Cognitive diagnostic models (CDMs) are a popular family of discrete latent variable models that model students’ mastery or deficiency of multiple fine-grained skills. CDMs have been most widely used to model categorical item response data such as binary or polytomous responses. With advances in technology and the emergence of varying test formats in modern educational assessments, new response types, including continuous responses such as response times, and count-valued responses from tests with repetitive tasks or eye-tracking sensors, have also become available. Variants of CDMs have been proposed recently for modeling such responses. However, whether these extended CDMs are identifiable and estimable is entirely unknown. We propose a very general cognitive diagnostic modeling framework for arbitrary types of multivariate responses with minimal assumptions, and establish identifiability in this general setting. Surprisingly, we prove that our general-response CDMs are identifiable under \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\textbf{Q}}$$\end{document}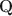 -matrix-based conditions similar to those for traditional categorical-response CDMs. Our conclusions set up a new paradigm of identifiable general-response CDMs. We propose an EM algorithm to efficiently estimate a broad class of exponential family-based general-response CDMs. We conduct simulation studies under various response types. The simulation results not only corroborate our identifiability theory, but also demonstrate the superior empirical performance of our estimation algorithms. We illustrate our methodology by applying it to a TIMSS 2019 response time dataset.
-matrix-based conditions similar to those for traditional categorical-response CDMs. Our conclusions set up a new paradigm of identifiable general-response CDMs. We propose an EM algorithm to efficiently estimate a broad class of exponential family-based general-response CDMs. We conduct simulation studies under various response types. The simulation results not only corroborate our identifiability theory, but also demonstrate the superior empirical performance of our estimation algorithms. We illustrate our methodology by applying it to a TIMSS 2019 response time dataset.