We consider a system with Poisson arrivals and independent and identically distributed service times, where requests in the system are served according to the state-dependent (Cohen's generalized) processor-sharing discipline, where each request receives a service capacity that depends on the actual number of requests in the system. For this system, we derive expressions as well as tight insensitive upper bounds for the moments of the conditional sojourn time of a request with given required service time. The bounds generalize and extend corresponding results, recently given for the single-server processor-sharing system in Cheung et al. (2006) and for the state-dependent processor-sharing system with exponential service times by the authors (2008). Analogous results hold for the waiting times. Numerical examples for the M/M/m-PS and M/D/m-PS systems illustrate the given bounds.

A particular queue, the general arrival, general service-time, infinite-server queue (GA/G/∞), is introduced and certain of its properties studied. Motivated by a life situation in which the interarrival times for service converge to 0, a different sort of regularity condition (involving a tail property of random measures) is imposed on the arrival process to prove various limit theorems. There are similarities to heavy-traffic theory.

For the distribution functions of the stationary actual waiting time and of the stationary virtual waiting time of the GI/G/l queueing system it is shown that the tails vary regularly at infinity if and only if the tail of the service time distribution varies regularly at infinity.

For sn the sum of n i.i.d. variables xi, i = 1, …, n it is shown that if E {x1} < 0 then the distribution of sup, s1s2, …] has a regularly varying tail at + ∞ if the tail of the distribution of x1 varies regularly at infinity and conversely, moreover 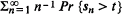varies regularly at + ∞.

In the appendix a lemma and its proof are given providing necessary and sufficient conditions for regular variation of the tail of a compound Poisson distribution.