We continue the study of the discrete-time risk model introduced by Picard et al. (2003). The cumulative loss process (St)t∊ℕ has independent and stationary increments, the increments per unit of time having nonnegative integer values with distribution {ai, i ∊ ℕ and mean ā. The premium receipt process (ck)k∊ℕ is deterministic, nonnegative and nonuniform; in addition, we assume it to be regular in order for there to exist a constant c > ā such that the deviation 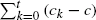 is bounded as the time t varies. We are interested in whether or not ruin occurs within a finite time. If T is the time of ruin, we obtain P(T = ∞) as the limit of P(T > t) as t → ∞, firstly in the particular case where c = 1/d for some positive d ∊ ℕ, and then in the general case for positive c under the condition that a0 > ½.
is bounded as the time t varies. We are interested in whether or not ruin occurs within a finite time. If T is the time of ruin, we obtain P(T = ∞) as the limit of P(T > t) as t → ∞, firstly in the particular case where c = 1/d for some positive d ∊ ℕ, and then in the general case for positive c under the condition that a0 > ½.

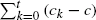 is bounded as the time
is bounded as the time 