Inquisitive first-order logic, InqBQ, is a system which extends classical first-order logic with formulas expressing questions. From a mathematical point of view, formulas in this logic express properties of sets of relational structures. This paper makes two contributions to the study of this logic. First, we describe an Ehrenfeucht–Fraïssé game for InqBQ and show that it characterizes the distinguishing power of the logic. Second, we use the game to study cardinality quantifiers in the inquisitive setting. That is, we study what statements and questions can be expressed in InqBQ about the number of individuals satisfying a given predicate. As special cases, we show that several variants of the question how many individuals satisfy 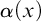$\alpha (x)$ are not expressible in InqBQ, both in the general case and in restriction to finite models.