1 results
Adjacency Preserving Maps on Hermitian Matrices
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1066
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
-
Hua’s fundamental theorem of the geometry of hermitian matrices characterizes bijective maps on the space of all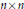
$n\times n$ hermitianmatrices preserving adjacency in both directions. The problem of possible improvements has been open for a while. There are three natural problems here. Do we need the bijectivity assumption? Can we replace the assumption of preserving adjacency in both directions by the weaker assumption of preserving adjacency in one direction only? Can we obtain such a characterization formaps acting between the spaces of hermitian matrices of different sizes? We answer all three questions for the complex hermitian matrices, thus obtaining the optimal structural result for adjacency preserving maps on hermitian matrices over the complex field.
