Search

Summary

We discuss the projectivity of the moduli space of semistable vector bundles on a curve of genus g ≥ 2. This is a classical result from the 1960s, obtained using geometric invariant theory. We outline a modern approach that combines the recent machinery of good moduli spaces with determinantal line bundle techniques. The crucial step producing an ample line bundle follows an argument by Faltings with improvements by Esteves–Popa. We hope to promote this approach as a blueprint for other projectivity arguments.

We prove a general criterion for an algebraic stack to admit a good moduli space. This result may be considered as a generalization of the Keel–Mori theorem, which guarantees the existence of a coarse moduli space for a separated Deligne–Mumford stack. We apply this result to prove that the moduli stacks 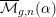$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$ parameterizing 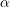$\unicode[STIX]{x1D6FC}$-stable curves introduced in [J. Alper et al., Second flip in the Hassett–Keel program: a local description, Compositio Math. 153 (2017), 1547–1583] admit good moduli spaces.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

3 - Projectivity of the moduli space of vector bundles on a curve

Summary

Second flip in the Hassett–Keel program: existence of good moduli spaces

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

3 - Projectivity of the moduli space of vector bundles on a curve

Summary

Second flip in the Hassett–Keel program: existence of good moduli spaces