This paper presents a comprehensive evaluation of reduced-order models (ROMs) for the determination of pressure coefficient distributions on supersonic and hypersonic bodies. The study investigates the limitations, aerodynamic precision and computational performance associated with various methodologies, ranging from simplistic Newtonian theory-based approaches to more advanced first and second-order shock-expansion theories. Validation is performed by comparing computed results with experimental and computational data for pressure distributions, drag and lift coefficients and centres of pressure for fundamental geometries and authentic vehicle design over a wide range of freestream conditions. The study also includes a comprehensive computational complexity analysis, demonstrating the superiority of finite-element ROM approaches over traditional finite-volume computational fluid dynamics (CFD) simulations. The primary objective of this paper is to scrutinise the extension of these methodological classes to the low supersonic regime. Hence, thermo-chemical reactions within the flow are disregarded, and the ideal gas law is adopted. A value of 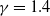 $\gamma = 1.4$ is chosen for consistency and comparability across the analyses. The proposed ROMs show remarkable potential for reducing high-speed simulation execution times by four orders of magnitude, maintaining accuracy within 20 per cent and as low as 1 per cent. The study unveils three key findings: first, the accuracy degradation of Newtonian-based theories for inclined elements, particularly around 45 degrees, and their reduced dependency on Mach number at large inclination. Secondly, the study presents novel insights into the impact of shock-wave-Mach-wave interactions on pressure distribution calculations, emphasising the Mach number as a crucial metric governing recompression effects. Lastly, the study demonstrates the exceptional accuracy of DeJarnette’s method, providing
$\gamma = 1.4$ is chosen for consistency and comparability across the analyses. The proposed ROMs show remarkable potential for reducing high-speed simulation execution times by four orders of magnitude, maintaining accuracy within 20 per cent and as low as 1 per cent. The study unveils three key findings: first, the accuracy degradation of Newtonian-based theories for inclined elements, particularly around 45 degrees, and their reduced dependency on Mach number at large inclination. Secondly, the study presents novel insights into the impact of shock-wave-Mach-wave interactions on pressure distribution calculations, emphasising the Mach number as a crucial metric governing recompression effects. Lastly, the study demonstrates the exceptional accuracy of DeJarnette’s method, providing 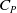 ${C_P}$ results within 2 per cent for a wide range of conditions, offering an attractive alternative to the Taylor-Maccoll equation.
${C_P}$ results within 2 per cent for a wide range of conditions, offering an attractive alternative to the Taylor-Maccoll equation.