We investigate the tower spectrum in the generalized Baire space, i.e., the set of lengths of towers in 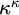$\kappa ^\kappa $. We show that both small and large tower spectra at all regular cardinals simultaneously are consistent. Furthermore, based on previous work by Bağ, the first author and Friedman, we prove that globally, a small tower spectrum is consistent with an arbitrarily large spectrum of maximal almost disjoint families. Finally, we show that any non-trivial upper bound on the tower spectrum in 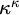$\kappa ^\kappa $ is consistent.

We study the values of the higher dimensional cardinal characteristics for sets of functions $f:\omega ^\omega \to \omega ^\omega $ introduced by the second author in [8]. We prove that while the bounding numbers for these cardinals can be strictly less than the continuum, the dominating numbers cannot. We compute the bounding numbers for the higher dimensional relations in many well known models of $\neg \mathsf {CH}$ such as the Cohen, random and Sacks models and, as a byproduct show that, with one exception, for the bounding numbers there are no $\mathsf {ZFC}$ relations between them beyond those in the higher dimensional Cichoń diagram. In the case of the dominating numbers we show that in fact they collapse in the sense that modding out by the ideal does not change their values. Moreover, they are closely related to the dominating numbers $\mathfrak {d}^\lambda _\kappa $.