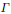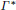A Dirac comb of point measures in Euclidean space with bounded complex weights that is supported on a lattice 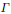 $\Gamma$ inherits certain general properties from the lattice structure. In particular, its autocorrelation admits a factorization into a continuous function and the uniformlattice Dirac comb, and its diffraction measure is periodic, with the dual lattice
$\Gamma$ inherits certain general properties from the lattice structure. In particular, its autocorrelation admits a factorization into a continuous function and the uniformlattice Dirac comb, and its diffraction measure is periodic, with the dual lattice 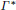 ${{\Gamma }^{*}}$ as lattice of periods. This statement remains true in the setting of a locally compact Abelian group whose topology has a countable base.
${{\Gamma }^{*}}$ as lattice of periods. This statement remains true in the setting of a locally compact Abelian group whose topology has a countable base.