1 results
A homotopy exact sequence for overconvergent isocrystals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 October 2021, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this article we prove exactness of the homotopy sequence of overconvergent fundamental groups for a smooth and projective morphism in characteristic p. We do so by first proving a corresponding result for rigid analytic varieties in characteristic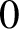
$0$, following dos Santos [dS15] in the algebraic case. In characteristic p, we then proceed by a series of reductions to the case of a liftable family of curves, where we can apply the rigid analytic result. We then use this to deduce a Lefschetz hyperplane theorem for convergent fundamental groups, as well as a comparison theorem with the étale fundamental group.
