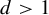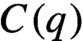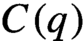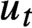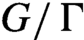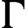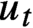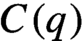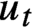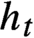We compute the gap distribution of directions of saddle connections for two classes of translation surfaces. One class will be the translation surfaces arising from gluing two identical tori along a slit. These yield the first explicit computations of gap distributions for non-lattice translation surfaces. We show that this distribution has support at zero and quadratic tail decay. We also construct examples of translation surfaces in any genus $d>1$ that have the same gap distribution as the gap distribution of two identical tori glued along a slit. The second class we consider are twice-marked tori and saddle connections between distinct marked points with a specific orientation. These results can be interpreted as the gap distribution of slopes of affine lattices. We obtain our results by translating the question of gap distributions to a dynamical question of return times to a transversal under the horocycle flow on an appropriate moduli space.

We introduce two properties: strong R-property and $C(q)$ -property, describing a special way of divergence of nearby trajectories for an abstract measure-preserving system. We show that systems satisfying the strong R-property are disjoint (in the sense of Furstenberg) with systems satisfying the $C(q)$ -property. Moreover, we show that if $u_t$ is a unipotent flow on $G/\Gamma $ with $\Gamma $ irreducible, then $u_t$ satisfies the $C(q)$ -property provided that $u_t$ is not of the form $h_t\times \operatorname {id}$ , where $h_t$ is the classical horocycle flow. Finally, we show that the strong R-property holds for all (smooth) time changes of horocycle flows and non-trivial time changes of bounded-type Heisenberg nilflows.

In L. W. Flinn’s PhD thesis published in 1972, the author conjectured that weakly expansive flows are also expansive flows. In this paper we use the horocycle flow on compact Riemann surfaces of constant negative curvature to show that Flinn’s conjecture is not true.

A classic result due to Furstenberg is the strict ergodicity of the horocycle flow for a compact hyperbolic surface. Strict ergodicity is unique ergodicity with respect to a measure of full support, and therefore it implies minimality. The horocycle flow has been previously studied on minimal foliations by hyperbolic surfaces on closed manifolds, where it is known not to be minimal in general. In this paper, we prove that for the special case of Riemannian foliations, strict ergodicity of the horocycle flow still holds. This, in particular, proves that this flow is minimal, which establishes a conjecture proposed by Matsumoto. The main tool is a theorem due to Coudène, which he presented as an alternative proof for the surface case. It applies to two continuous flows defining a measure-preserving action of the affine group of the line on a compact metric space, precisely matching the foliated setting. In addition, we briefly discuss the application of Coudène’s theorem to other kinds of foliations.