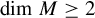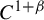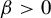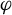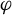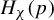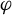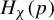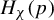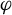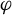The manifold M is a Riemannian, boundaryless, and compact manifold with 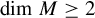$\dim M\geq 2$, and f is a 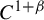$C^{1+\beta }$ (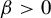$\kern0.3pt\beta>0$) diffeomorphism of M. 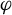$\varphi $ is a Hölder continuous potential on M. We construct an invariant and absolutely continuous family of measures (with transformation relations defined by 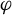$\varphi $), which sit on local unstable leaves. We present two main applications. 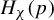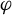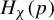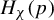First, given an ergodic homoclinic class $H_\chi (p)$, we prove that $\varphi $ admits a local equilibrium state on $H_\chi (p)$ if and only if $\varphi $ is ‘recurrent on $H_\chi (p)$’ (a condition tested by counting periodic points), and one of the leaf measures gives a positive measure to a set of positively recurrent hyperbolic points; and if an equilibrium measure exists, the said invariant and absolutely continuous family of measures constitute as its conditional measures. An immediate corollary is the local product structure of hyperbolic equilibrium states. Second, we prove a Ledrappier–Young property for hyperbolic equilibrium states: if 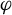$\varphi $ admits a conformal family of leaf measures and a hyperbolic local equilibrium state, then the leaf measures of the invariant family (respective to 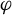$\varphi $) are equivalent to the conformal measures (on a full measure set). This extends the celebrated result by Ledrappier and Young for hyperbolic Sinai–Ruelle–Bowen measures, which states that a hyperbolic equilibrium state of the geometric potential (with pressure zero) has conditional measures on local unstable leaves which are absolutely continuous with respect to the Riemannian volume of these leaves.

In the first part of the paper, we introduce notions of asymptotic continuous orbit equivalence and asymptotic conjugacy in Smale spaces and characterize them in terms of their asymptotic Ruelle algebras with their dual actions. In the second part, we introduce a groupoid $C^{\ast }$-algebra that is an extended version of the asymptotic Ruelle algebra from a Smale space and study the extended Ruelle algebras from the view points of Cuntz–Krieger algebras. As a result, the asymptotic Ruelle algebra is realized as a fixed point algebra of the extended Ruelle algebra under certain circle action.

We present a new construction of the entropy-maximizing, invariant probability measure on a Smale space (the Bowen measure). Our construction is based on points that are unstably equivalent to one given point, and stably equivalent to another, i.e., heteroclinic points. The spirit of the construction is similar to Bowen's construction from periodic points, though the techniques are very different. We also prove results about the growth rate of certain sets of heteroclinic points, and about the stable and unstable components of the Bowen measure. The approach we take is to prove results through direct computation for the case of a Shift of Finite type, and then use resolving factor maps to extend the results to more general Smale spaces.