2 results
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
-
We study the dynamics induced by homogeneous polynomials on Banach spaces. It is known that no homogeneous polynomial defined on a Banach space can have a dense orbit. We show a simple and natural example of a homogeneous polynomial with an orbit that is at the same time
$\unicode[STIX]{x1D6FF}$-dense (the orbit meets every ball of radius 
$\unicode[STIX]{x1D6FF}$), weakly dense and such that 
$\unicode[STIX]{x1D6E4}\cdot \text{Orb}_{P}(x)$ is dense for every 
$\unicode[STIX]{x1D6E4}\subset \mathbb{C}$ that either is unbounded or has 0 as an accumulation point. Moreover, we generalize the construction to arbitrary infinite-dimensional separable Banach spaces. To prove this, we study Julia sets of homogeneous polynomials on Banach spaces.
Hypercyclic and mixing operator semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 27 June 2011, pp. 761-782
-
- Article
-
- You have access
- Export citation
-
We describe a class of topological vector spaces admitting a mixing uniformly continuous operator group
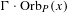
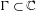
with holomorphic dependence on the parameter t. This result builds on those existing in the literature. We also describe a class of topological vector spaces admitting no supercyclic strongly continuous operator semigroups 
.
with holomorphic dependence on the parameter 
.