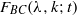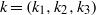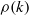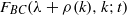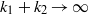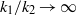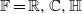Refine search
Actions for selected content:
2 results
6 - Elliptic Hypergeometric Functions Associated with Root Systems
-
-
- Book:
- Encyclopedia of Special Functions: The Askey-Bateman Project
- Published online:
- 30 September 2020
- Print publication:
- 15 October 2020, pp 159-186
-
- Chapter
- Export citation
Limit transition between hypergeometric functions of type BC and type A
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 19 June 2013, pp. 1381-1400
- Print publication:
- August 2013
-
- Article
- Export citation