1 results
Fcfs infinite bipartite matching of servers and customers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-730
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
-
We consider an infinite sequence of customers of types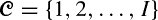
and an infinite sequence of servers of types 
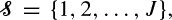where a server of type j can serve a subset of customer types C(j) and where a customer of type i can be served by a subset of server types S(i). We assume that the types of customers and servers in the infinite sequences are random, independent, and identically distributed, and that customers and servers are matched according to their order in the sequence, on a first-come–first-served (FCFS) basis. We investigate this process of infinite bipartite matching. In particular, we are interested in the rate ri,j that customers of type i are assigned to servers of type j. We present a countable state Markov chain to describe this process, and for some previously unsolved instances, we prove ergodicity and existence of limiting rates, and calculate ri,j.
and an infinite sequence of servers of types 
where a server of type 