We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let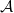 
$\mathcal{A}$ be a locally noetherian Grothendieck category. We classify all full subcategories of 
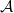$\mathcal{A}$ which are thick and closed under taking arbitrary direct sums and injective envelopes by injective spectrum. This result gives a generalization from the commutative noetherian ring to the locally noetherian Grothendieck category.
