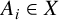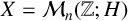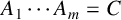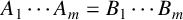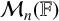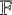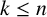Refine search
Actions for selected content:
2 results
4 - Symbolic dynamics and the stable algebra of matrices
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 266-422
-
- Chapter
- Export citation
SOME COUNTING QUESTIONS FOR MATRIX PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 32-43
- Print publication:
- August 2024
-
- Article
- Export citation