We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that compatible systems of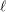 
$\ell$-adic sheaves on a scheme of finite type over the ring of integers of a local field are compatible along the boundary up to stratification. This extends a theorem of Deligne on curves over a finite field. As an application, we deduce the equicharacteristic case of classical conjectures on 
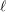$\ell$-independence for proper smooth varieties over complete discrete valuation fields. Moreover, we show that compatible systems have compatible ramification. We also prove an analogue for integrality along the boundary.
