We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that the total variation mixing time is not quasi-isometry invariant, even for Cayley graphs. Namely, we construct a sequence of pairs of Cayley graphs with maps between them that twist the metric in a bounded way, while the ratio of the two mixing times goes to infinity. The Cayley graphs serving as an example have unbounded degrees. For non-transitive graphs, we construct bounded degree graphs for which the mixing time from the worst starting point for one graph is asymptotically smaller than the mixing time from the best starting point of the random walk on a network obtained by increasing some of the edge weights from 1 to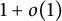 
$1+o(1)$.
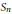${{S}_{n}}$ Using the Interchange Process
Inspired by Aldous' conjecture for the spectral gap of the interchange process and its recent resolution by Caputo, Liggett, and Richthammer, we define an associated order 
$\prec $ on the irreducible representations of ${{S}_{n}}$. Aldous' conjecture is equivalent to certain representations being comparable in this order, and hence determining the “Aldous order” completely is a generalized question. We show a few additional entries for this order.
